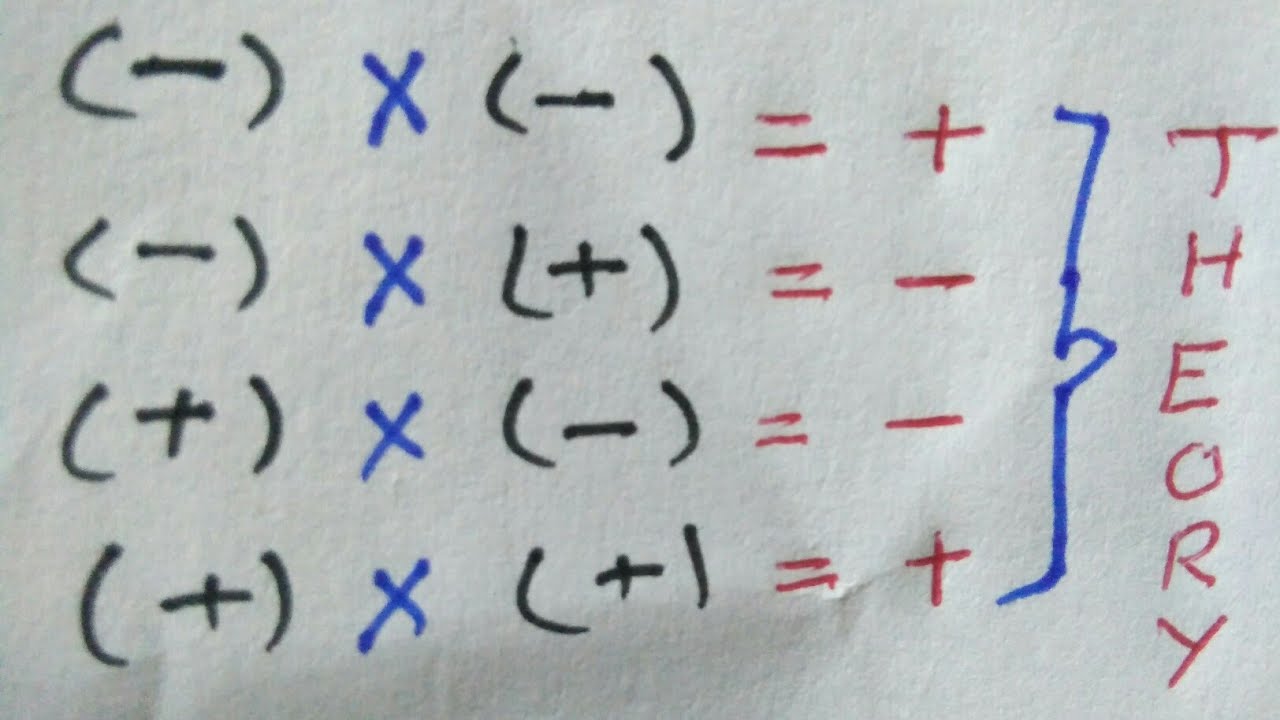Understanding The Concept Of Negative Times A Positive Equals

Mathematics often poses questions that can stump even the most seasoned learners, but understanding basic operations is crucial for mastering more complex concepts. One such fundamental operation is the multiplication of negative and positive numbers. It's a common misconception that multiplying a negative by a positive yields a positive result. In fact, this operation demonstrates a fascinating aspect of mathematical logic and number theory that is essential for students and professionals alike. In this article, we will unravel the mystery behind the phrase "negative times a positive equals," exploring its implications and applications in various fields.

The concept of negative times a positive equals can be simplified into a straightforward rule: when you multiply a negative number by a positive number, the result is always negative. This principle not only applies in mathematics but also serves as a metaphor in life, illustrating how negative experiences can influence positive situations. By delving deeper into this concept, we can better comprehend its significance in both theoretical and practical scenarios.

As we explore the intricacies of negative and positive multiplication, we will answer several key questions about this mathematical operation. From understanding the basic rules to exploring practical applications, this article aims to provide clarity and insight into the world of numbers. Let's embark on this journey to uncover the truth behind negative times a positive equals!

What Does Negative Times a Positive Equals?

When we talk about negative times a positive equals, we are referring to a fundamental rule in arithmetic. Multiplying a negative number by a positive number results in a negative product. For instance, if you take -3 (negative three) and multiply it by +4 (positive four), the calculation would look like this:

• -3 × +4 = -12

The result, -12, is negative, which reinforces the idea that negative times a positive equals a negative.

Why is Negative Times a Positive Important in Mathematics?

Understanding why negative times a positive equals negative is crucial for various mathematical applications. This foundational knowledge is essential for students as they progress to more advanced topics such as algebra, calculus, and beyond. Here are some reasons why this concept is significant:

• It helps in solving equations.
• It is essential for understanding the properties of numbers.
• It aids in graphing functions on a coordinate plane.
• It assists in real-world applications, such as calculating profit and loss.

How Can We Visualize Negative Times a Positive?

Visualizing the multiplication of negative and positive numbers can help in comprehending the concept better. One effective way to represent this is through a number line. On a number line, positive numbers extend to the right of zero, while negative numbers extend to the left.

Imagine starting at a positive point on the number line and moving backward (to the left) based on the value of the negative number. Each step you take backwards represents the multiplication of a negative number by a positive number, resulting in a negative product.

What Are Some Real-World Examples of Negative Times a Positive?

The concept of negative times a positive equals negative can be observed in various real-life situations. Here are a few examples to illustrate this principle:

• Financial Transactions: If a company has a debt of $5,000 (negative amount) and has 3 investors (positive factor), the total debt owed would be -5,000 × 3 = -15,000. This reflects an increasing debt.
• Temperature Changes: If the temperature drops from a positive value, say 10 degrees, by a negative 5 degrees, the resulting temperature would be 10 + (-5) = 5 degrees, which is still positive. However, if the temperature were to drop from 0 to -5, that would be a negative change.
• Distance or Speed: If a car is moving in the opposite direction (negative speed) at a rate of 60 mph (positive rate), the effective speed would be -60 mph, indicating backward movement.

How Does Negative Times a Positive Relate to Algebra?

In algebra, the principle of negative times a positive equals negative is applied when solving equations. For example, when simplifying expressions or solving for variables, understanding how to handle negative and positive coefficients is essential.

Consider the equation 2x + (-3) = 0. In this case, you must recognize that subtracting a positive number (3) will have the same effect as multiplying by a negative number, leading to a negative solution.

What Are Common Misconceptions About Negative Times a Positive?

Despite its simplicity, there are several common misconceptions surrounding the multiplication of negative and positive numbers. Here are a few:

• Many people mistakenly believe that a negative times a positive equals a positive result. This stems from a misunderstanding of the rules of multiplication.
• Some learners struggle with the concept of negative numbers, leading to confusion in calculations involving negative and positive values.
• Others may not recognize the importance of this principle in real-world applications, such as finance and temperature measurement.

How Can We Teach Negative Times a Positive Equals Effectively?

Teaching the concept of negative times a positive equals can be engaging and informative. Here are some effective strategies:

• Use visual aids such as number lines and graphs to illustrate the concept.
• Incorporate real-world examples to make the learning experience relatable.
• Encourage hands-on activities where students can practice multiplication with negative and positive numbers.
• Use interactive games or quizzes to reinforce learning and engagement.

Conclusion: The Importance of Understanding Negative Times a Positive Equals

In conclusion, the concept of negative times a positive equals negative is a fundamental principle in mathematics that extends beyond mere calculations. It plays a crucial role in various fields, from finance to science, and serves as a foundation for more advanced mathematical concepts. By embracing this rule and understanding its applications, we can enhance our mathematical proficiency and tackle complex problems with confidence.

So, the next time you encounter the phrase "negative times a positive equals," remember the significance of this operation and how it influences both theoretical and practical scenarios in our lives.